Preprocess¶

The module of preprocess contains methods that are processes that could be made to data before training.

Visualize Feature¶

This method was created due a quick solution to long time calculation of Pandas Profiling. This method give a quick visualization with small latency time.

preprocess.visualize_feature(series: pandas.core.series.Series, remove_na: bool = False, *, ax: Optional[matplotlib.axes._axes.Axes] = None, **kwargs) → matplotlib.axes._axes.Axes[source]¶

Visualize a feature series:

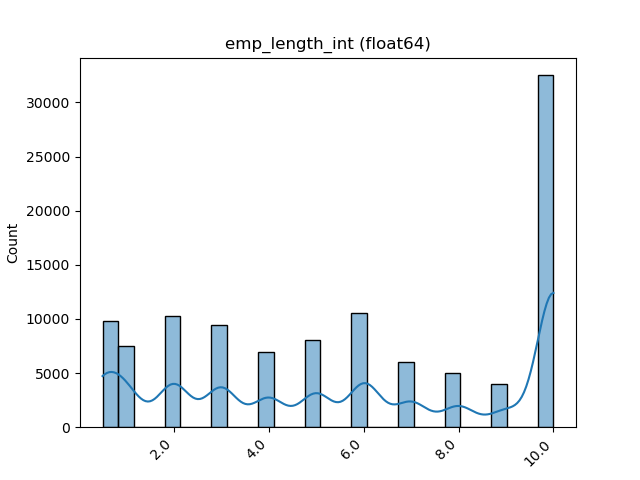
If the feature is float then the method plots the distribution plot.
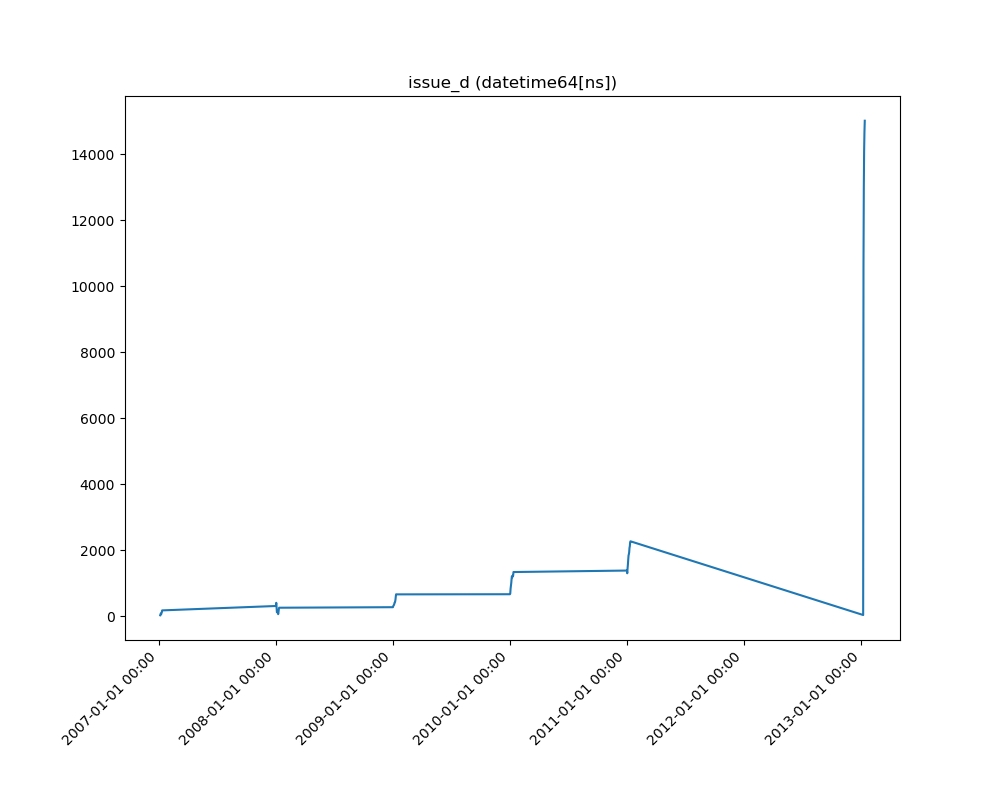
If the feature is datetime then the method plots a line plot of progression of amount thought time.
If the feature is object, categorical, boolean or integer then the method plots count plot (histogram).

Parameters:	series – the data series. remove_na – True to ignore NA values when plotting; False otherwise. ax – Axes in which to draw the plot, otherwise use the currently-active Axes. kwargs – other keyword arguments All other keyword arguments are passed to `matplotlib.axes.Axes.pcolormesh()`.
Returns:	Returns the Axes object with the plot drawn onto it.

Code Example¶

The example uses a small sample from of a dataset from kaggle, which a dummy bank provides loans.

Let’s see how to use the code:

import pandas

from matplotlib import pyplot

from ds_utils.preprocess import visualize_feature

loan_frame = pandas.read_csv(path/to/dataset, encoding="latin1", nrows=11000,
                             parse_dates=["issue_d"])
loan_frame = loan_frame.drop("id", axis=1)

visualize_features(loan_frame["some feature"])

pyplot.show()

For ech different type of feature a different graph will be generated:

Float¶

A distribution plot is shown:

Datetime Series¶

A line plot is shown:

Object, Categorical, Boolean or Integer¶

A count plot is shown.

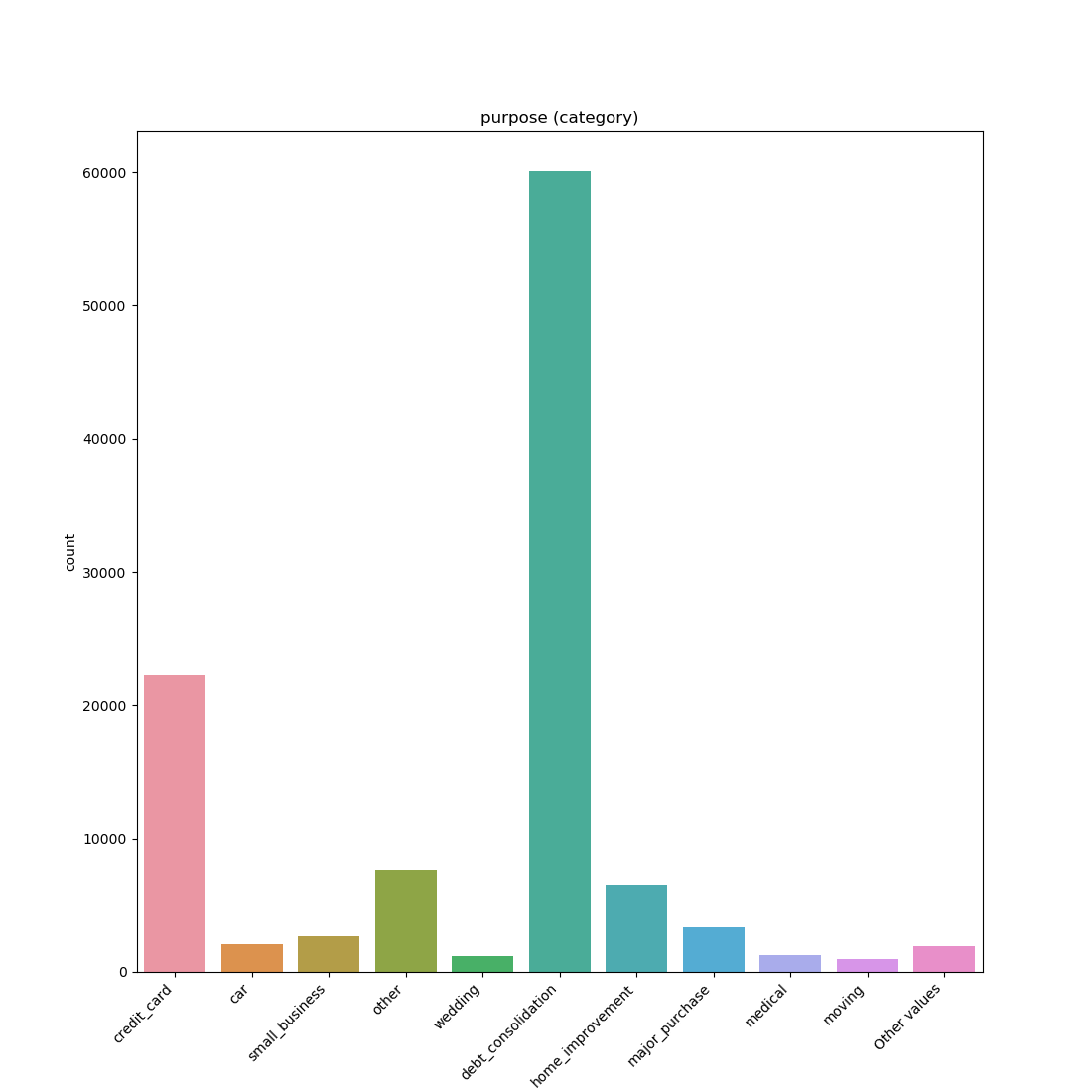
Categorical / Object:

If the categorical / object feature has more than 10 unique values, then the 10 most common values are shown and the other are labeled “Other Values”.

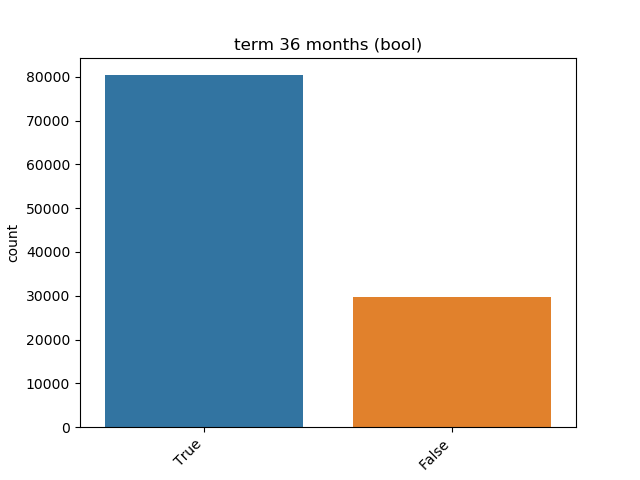
Boolean:

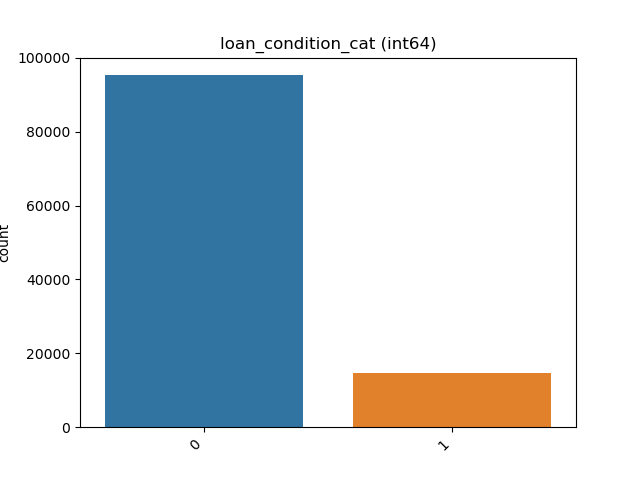
Integer:

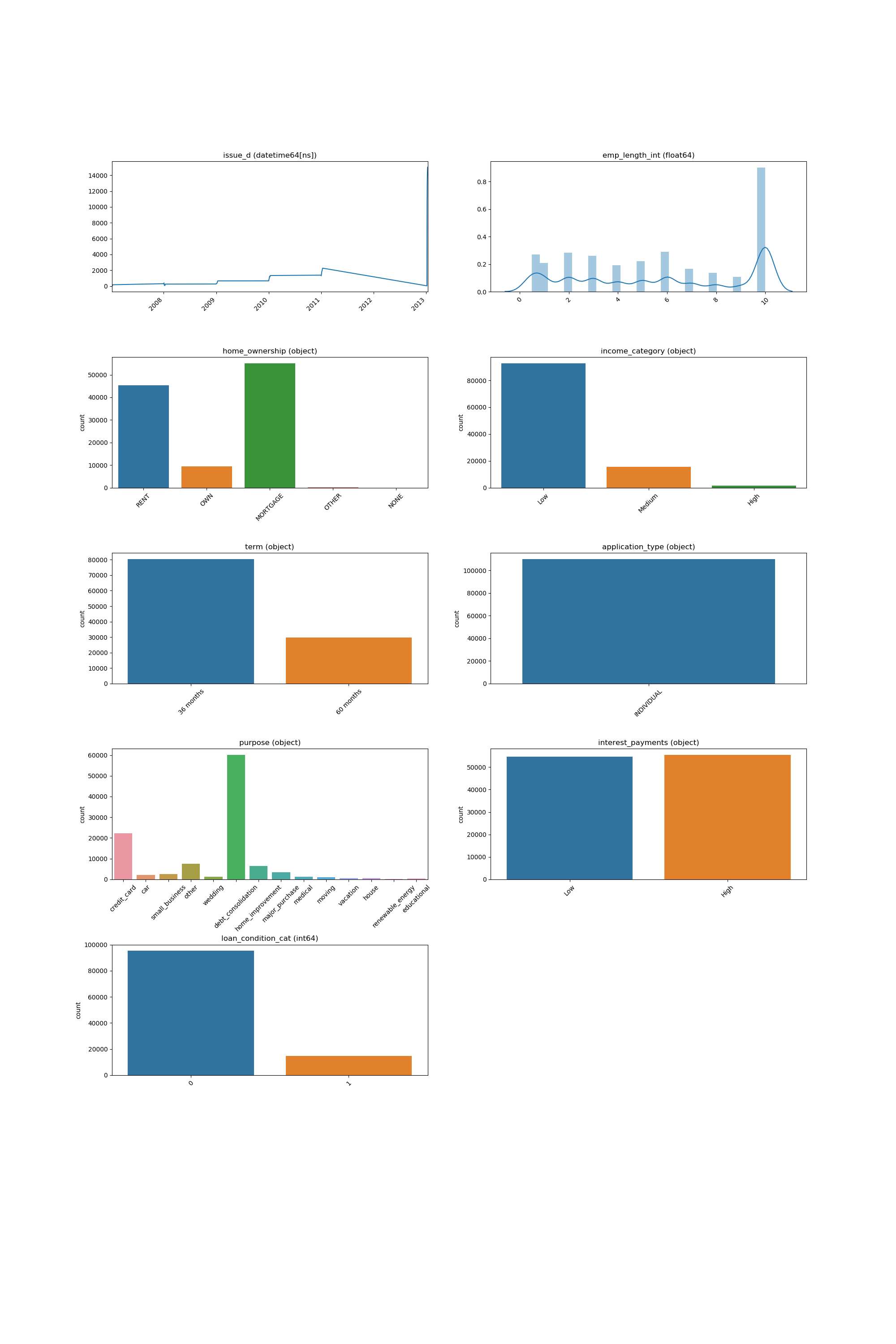
Looping Over All the Features¶

This code example shows how a loop can be constructed in order to show all of features:

import pandas

from matplotlib import pyplot

from ds_utils.preprocess import visualize_feature


loan_frame = pandas.read_csv(path/to/dataset, encoding="latin1", nrows=11000,
                             parse_dates=["issue_d"])
loan_frame = loan_frame.drop("id", axis=1)

figure, axes = pyplot.subplots(5, 2)
axes = axes.flatten()
figure.set_size_inches(18, 30)

features = loan_frame.columns
i = 0

for feature in features:
    visualize_feature(loan_frame[feature], ax=axes[i])
    i += 1

figure.delaxes(axes[9])
pyplot.subplots_adjust(hspace=0.5)
pyplot.show()

And the following image will be shown:

Get Correlated Features¶

preprocess.get_correlated_features(data_frame: pandas.core.frame.DataFrame, features: List[str], target_feature: str, threshold: float = 0.95, method: Union[str, Callable] = 'pearson', min_periods: Optional[int] = 1) → pandas.core.frame.DataFrame[source]¶

Calculate which features correlated above a threshold and extract a data frame with the correlations and correlation to the target feature.

Parameters:

data_frame – the data frame.
features – list of features names.
target_feature – name of target feature.
threshold – the threshold (default 0.95).
method –
{‘pearson’, ‘kendall’, ‘spearman’} or callable

Method of correlation:
- pearson : standard correlation coefficient
- kendall : Kendall Tau correlation coefficient
- spearman : Spearman rank correlation
- callable: callable with input two 1d ndarrays and returning a float. Note that the returned matrix from corr will have 1 along the diagonals and will be symmetric regardless of the callable’s behavior.
min_periods – Minimum number of observations required per pair of columns to have a valid result. Currently only available for Pearson and Spearman correlation.

Returns:

data frame with the correlations and correlation to the target feature.

Code Example¶

The example uses a small sample from of a dataset from kaggle, which a dummy bank provides loans.

Let’s see how to use the code:

import pandas
from ds_utils.preprocess import get_correlated_features


loan_frame = pandas.read_csv(path/to/dataset, encoding="latin1", nrows=30)
target = "loan_condition_cat"
features = train.columns.drop("loan_condition_cat", "issue_d", "application_type").tolist()
correlations = get_correlated_features(pandas.get_dummies(loan_frame), features, target)
print(correlations)

The following table will be the output:

level_0	level_1	level_0_level_1_corr	level_0_target_corr	level_1_target_corr
income_category_Low	income_category_Medium	1.0	0.1182165609358650	0.11821656093586504
term_ 36 months	term_ 60 months	1.0	0.1182165609358650	0.11821656093586504
interest_payments_High	interest_payments_Low	1.0	0.1182165609358650	0.11821656093586504

Visualize Correlations¶

This method was created due a quick solution to long time calculation of Pandas Profiling. This method give a quick visualization with small latency time.

preprocess.visualize_correlations(data: pandas.core.frame.DataFrame, method: Union[str, Callable] = 'pearson', min_periods: Optional[int] = 1, *, ax: Optional[matplotlib.axes._axes.Axes] = None, **kwargs) → matplotlib.axes._axes.Axes[source]¶

Compute pairwise correlation of columns, excluding NA/null values, and visualize it with heat map. Original code

Parameters:

data – the data frame, were each feature is a column.
method –
{‘pearson’, ‘kendall’, ‘spearman’} or callable

Method of correlation:
- pearson : standard correlation coefficient
- kendall : Kendall Tau correlation coefficient
- spearman : Spearman rank correlation
- callable: callable with input two 1d ndarrays and returning a float. Note that the returned matrix from corr will have 1 along the diagonals and will be symmetric regardless of the callable’s behavior.
min_periods – Minimum number of observations required per pair of columns to have a valid result. Currently only available for Pearson and Spearman correlation.
ax – Axes in which to draw the plot, otherwise use the currently-active Axes.
kwargs –
other keyword arguments

All other keyword arguments are passed to matplotlib.axes.Axes.pcolormesh().

Returns:

Returns the Axes object with the plot drawn onto it.

Code Example¶

For this example I created a dummy data set. You can find the data at the resources directory in the packages tests folder.

Let’s see how to use the code:

import pandas

from matplotlib import pyplot

from ds_utils.preprocess import visualize_correlations


data_1M = pandas.read_csv(path/to/dataset)
visualize_correlations(data_1M)
pyplot.show()

And the following image will be shown:

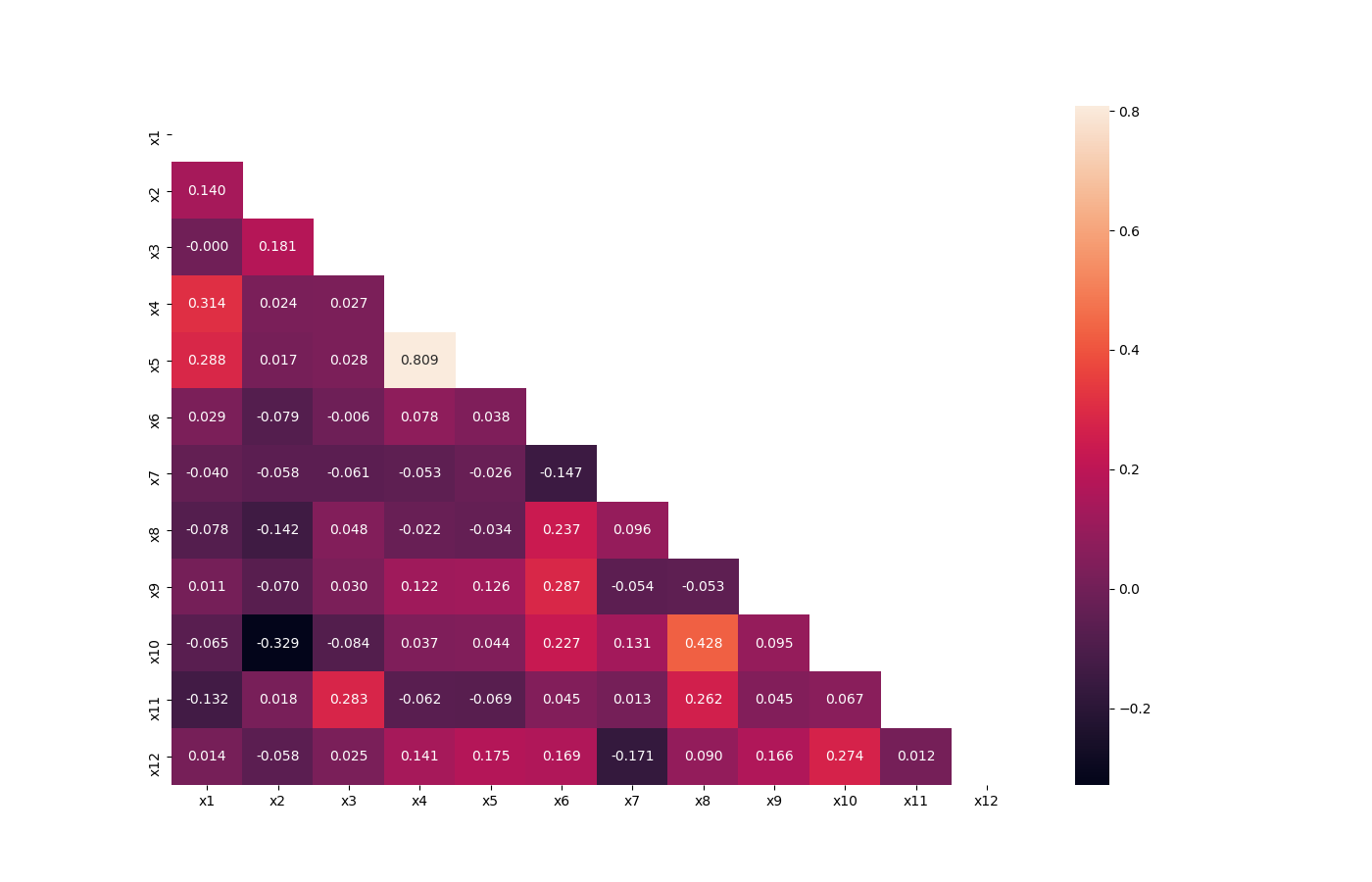
Plot Correlation Dendrogram¶

This method was created due the lack of maintenance of the package EthicalML / xai.

preprocess.plot_correlation_dendrogram(data: pandas.core.frame.DataFrame, correlation_method: Union[str, Callable] = 'pearson', min_periods: Optional[int] = 1, cluster_distance_method: Union[str, Callable] = 'average', *, ax: Optional[matplotlib.axes._axes.Axes] = None, **kwargs) → matplotlib.axes._axes.Axes[source]¶

Plot dendrogram of a correlation matrix. This consists of a chart that that shows hierarchically the variables that are most correlated by the connecting trees. The closer to the right that the connection is, the more correlated the features are.

Parameters:

data – the data frame, were each feature is a column.
correlation_method –
{‘pearson’, ‘kendall’, ‘spearman’} or callable

Method of correlation:
- pearson : standard correlation coefficient
- kendall : Kendall Tau correlation coefficient
- spearman : Spearman rank correlation
- callable: callable with input two 1d ndarrays and returning a float. Note that the returned matrix from corr will have 1 along the diagonals and will be symmetric regardless of the callable’s behavior.
min_periods – Minimum number of observations required per pair of columns to have a valid result. Currently only available for Pearson and Spearman correlation.
cluster_distance_method –
The following are methods for calculating the distance between the newly formed cluster.

Methods of linkage:
- single: This is also known as the Nearest Point Algorithm.
- complete: This is also known by the Farthest Point Algorithm or Voor Hees Algorithm.
- average:
\[d(u,v) = \sum_{ij} \frac{d(u[i], v[j])}{(|u|*|v|)}\]

This is also called the UPGMA algorithm.
- weighted:
\[d(u,v) = (dist(s,v) + dist(t,v))/2\]

where cluster u was formed with cluster s and t and v is a remaining cluster in the forest. (also called WPGMA)
- centroid: Euclidean distance between the centroids
- median: This is also known as the WPGMC algorithm.
- ward: uses the Ward variance minimization algorithm.
see scipy.cluster.hierarchy.linkage for more information.
ax – Axes in which to draw the plot, otherwise use the currently-active Axes.
kwargs –
other keyword arguments

All other keyword arguments are passed to matplotlib.axes.Axes.pcolormesh().

Returns:

Returns the Axes object with the plot drawn onto it.

Code Example¶

For this example I created a dummy data set. You can find the data at the resources directory in the packages tests folder.

Let’s see how to use the code:

import pandas

from matplotlib import pyplot

from ds_utils.preprocess import plot_correlation_dendrogram


data_1M = pandas.read_csv(path/to/dataset)
plot_correlation_dendrogram(data_1M)
pyplot.show()

And the following image will be shown:

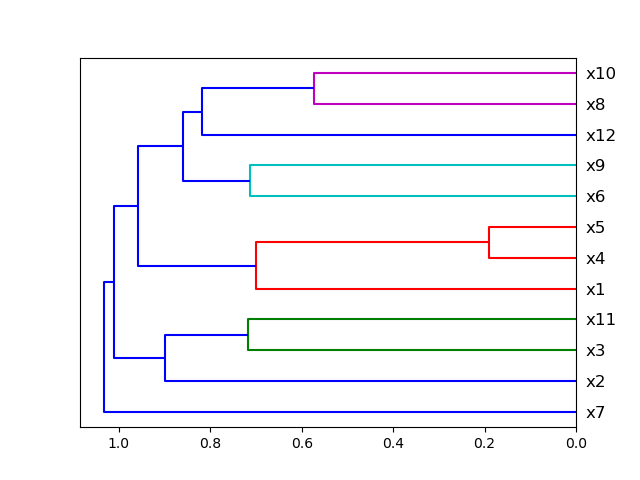
Plot Features’ Interaction¶

This method was created due a quick solution to long time calculation of Pandas Profiling. This method give a quick visualization with small latency time.

preprocess.plot_features_interaction(feature_1: str, feature_2: str, data: pandas.core.frame.DataFrame, *, ax: Optional[matplotlib.axes._axes.Axes] = None, **kwargs) → matplotlib.axes._axes.Axes[source]¶

Plots the joint distribution between two features:

If both features are either categorical, boolean or object then the method plots the shared histogram.
If one feature is either categorical, boolean or object and the other is numeric then the method plots a boxplot chart.
If one feature is datetime and the other is numeric or datetime then the method plots a line plot graph.
If one feature is datetime and the other is either categorical, boolean or object the method plots a violin plot (combination of boxplot and kernel density estimate).
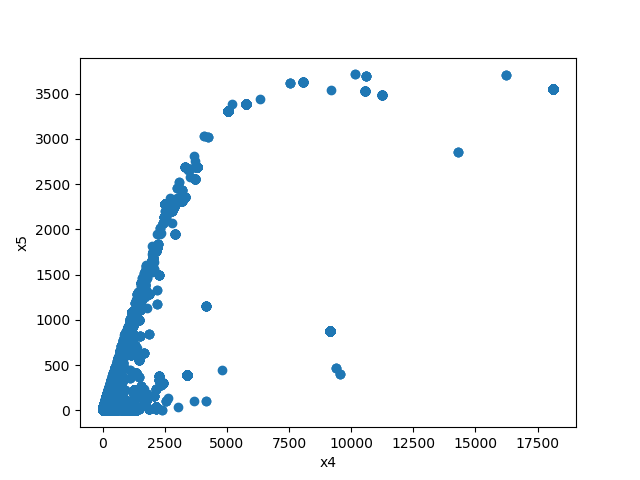
If both features are numeric then the method plots scatter graph.

Parameters:	feature_1 – the name of the first feature. feature_2 – the name of the second feature. data – the data frame, were each feature is a column. ax – Axes in which to draw the plot, otherwise use the currently-active Axes. kwargs – other keyword arguments All other keyword arguments are passed to `matplotlib.axes.Axes.pcolormesh()`.
Returns:	Returns the Axes object with the plot drawn onto it.

Code Example¶

For this example I created a dummy data set. You can find the data at the resources directory in the packages tests folder.

Let’s see how to use the code:

import pandas

from matplotlib import pyplot

from ds_utils.preprocess import plot_features_interaction


data_1M = pandas.read_csv(path/to/dataset)
plot_features_interaction("x7", "x10", data_1M)
pyplot.show()

For each different combination of features types a different plot will be shown:

Both Features are Numeric¶

A scatter plot of the shared distribution is shown:

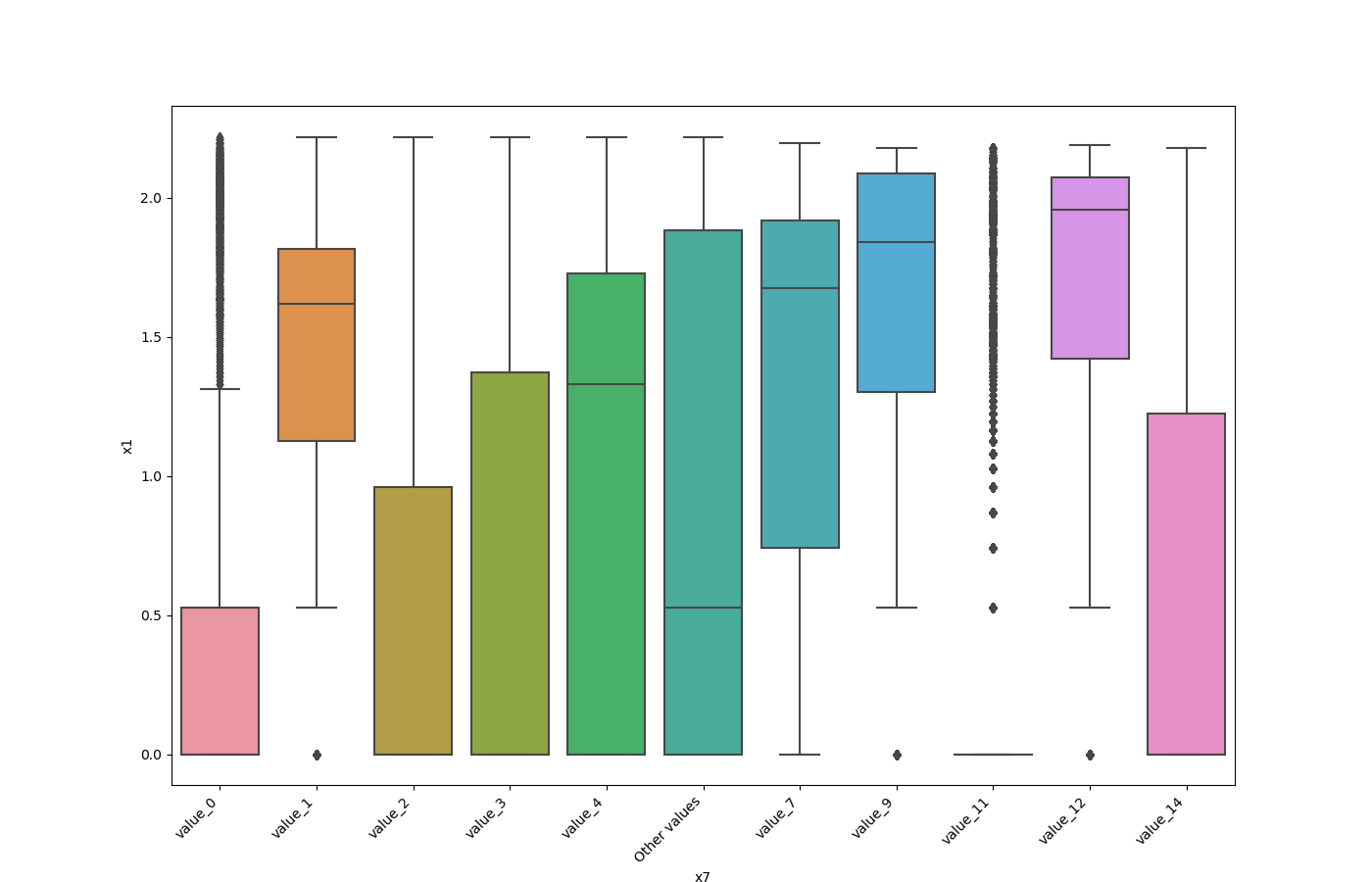
One Feature is Numeric and The Other is Categorical¶

If one feature is numeric, but the the other is either an object, a category or a bool, then a box plot is shown. In the plot it can be seen for each unique value of the category feature what is the distribution of the numeric feature. If the categorical feature has more than 10 unique values, then the 10 most common values are shown and the other are labeled “Other Values”.

Here is an example for boolean feature plot:

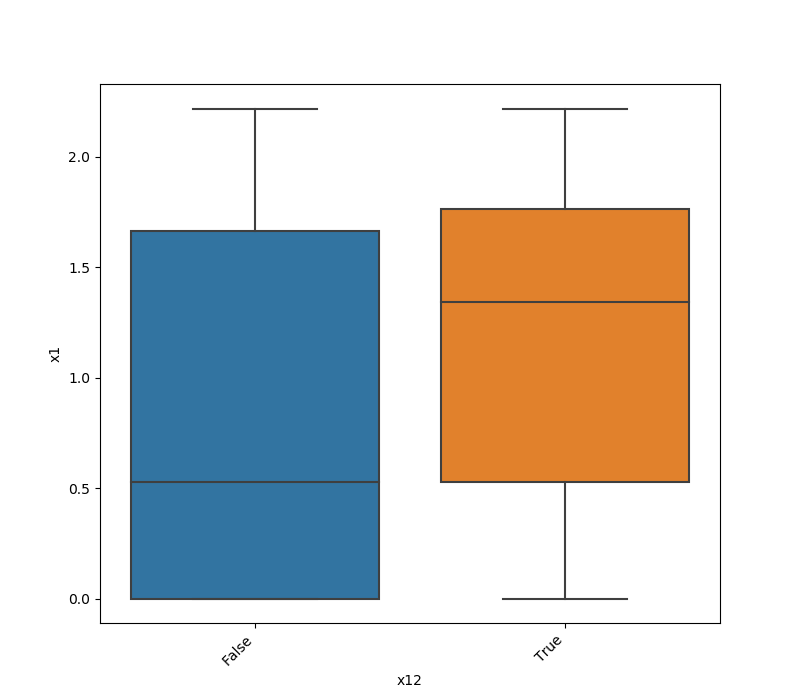
Both Features are Categorical¶

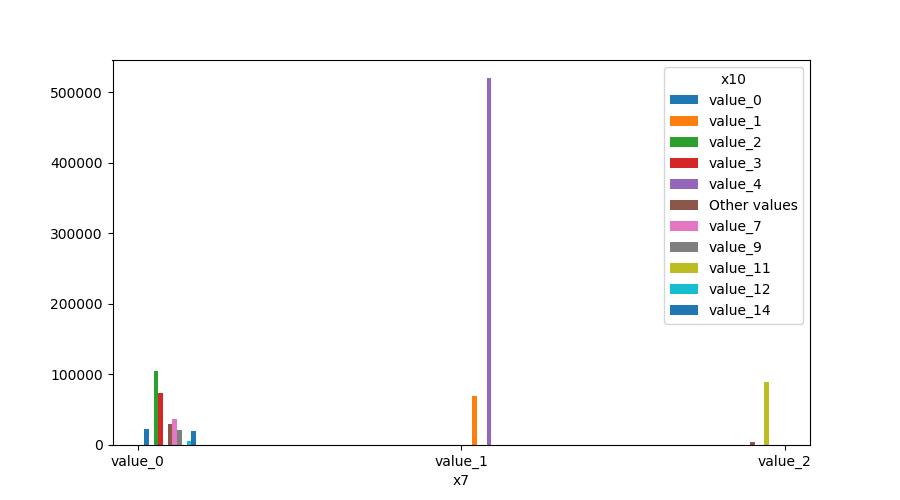
A shared histogram will be shown. If one or both features have more than 10 unique values, then the 10 most common values are shown and the other are labeled “Other Values”.

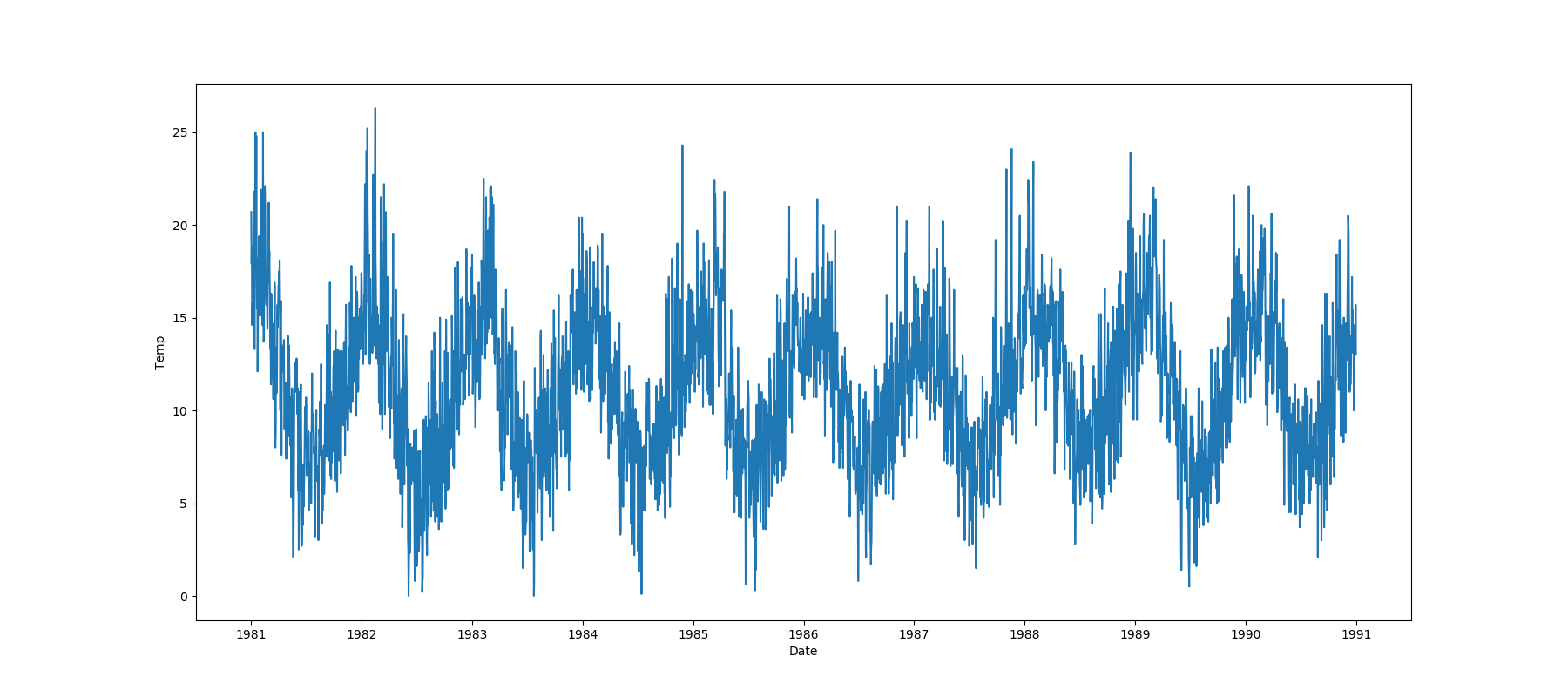
One Feature is Datetime Series and the Other is Numeric or Datetime Series¶

A line plot where the datetime series is at x axis is shown:

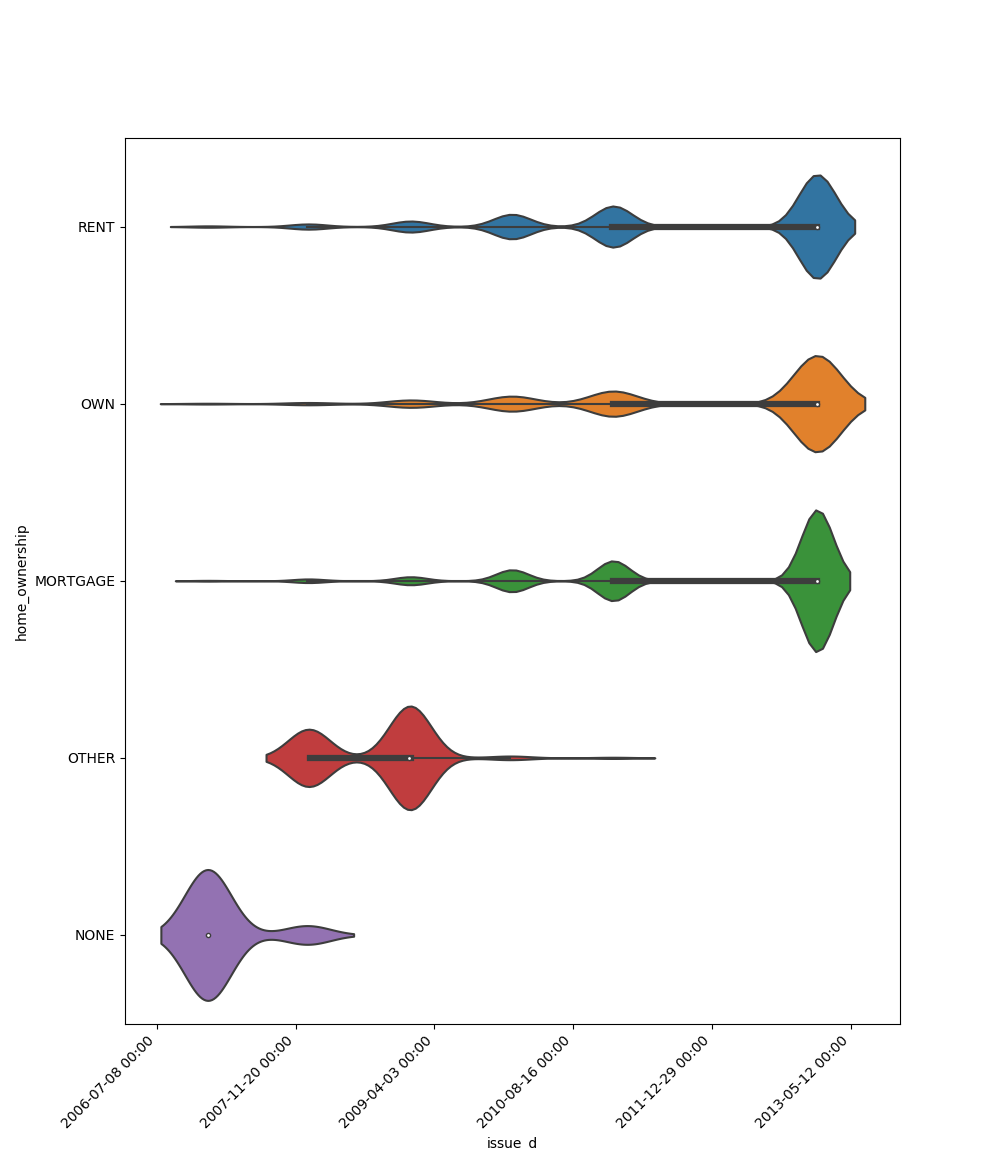
One Feature is Datetime Series and the Other is Categorical¶

If one feature is datetime series, but the the other is either an object, a category or a bool, then a violin plot is shown. Violin plot is a combination of boxplot and kernel density estimate. If the categorical feature has more than 10 unique values, then the 10 most common values are shown and the other are labeled “Other Values”. The datetime series will be at x axis:

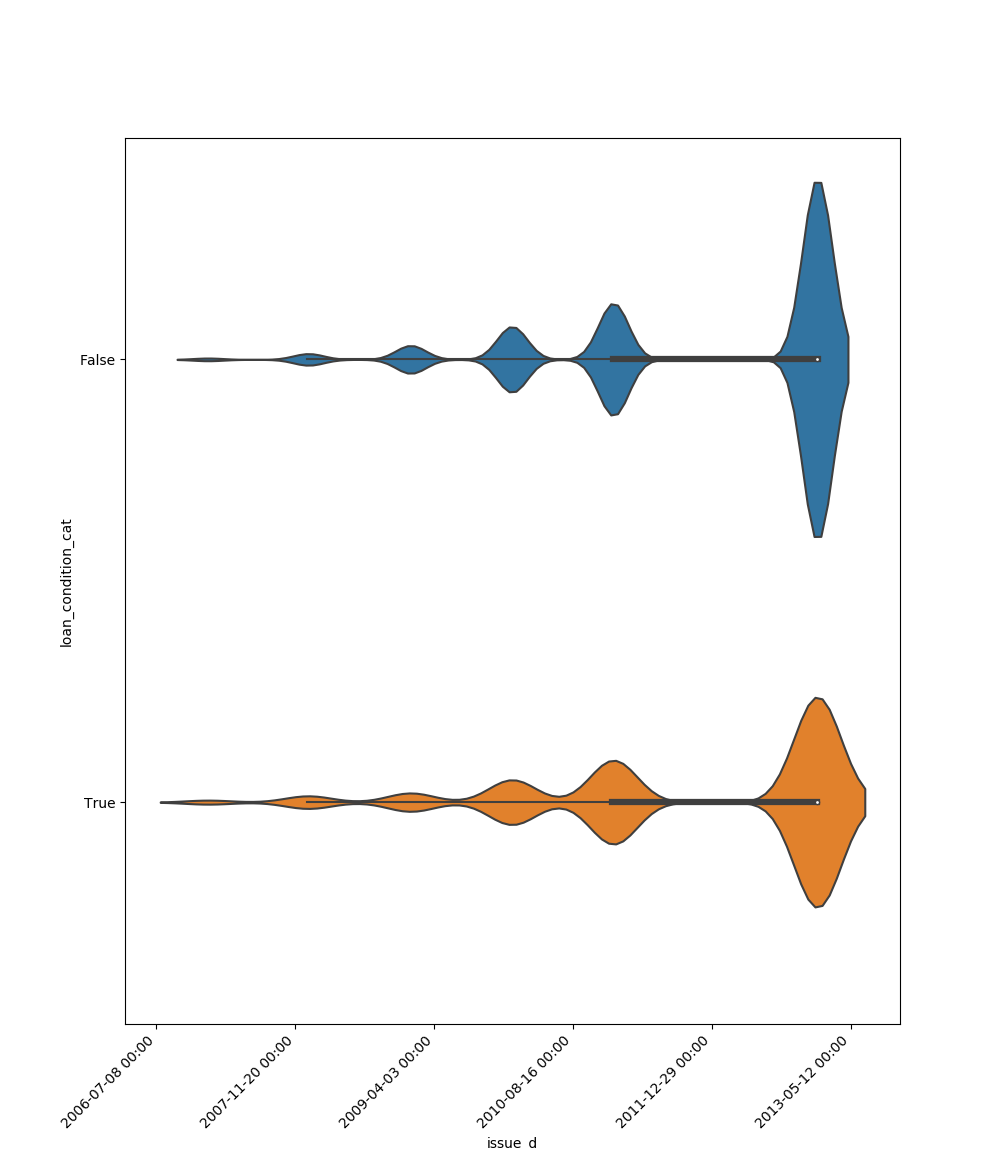
Here is an example for boolean feature plot:

Looping One Feature over The Others¶

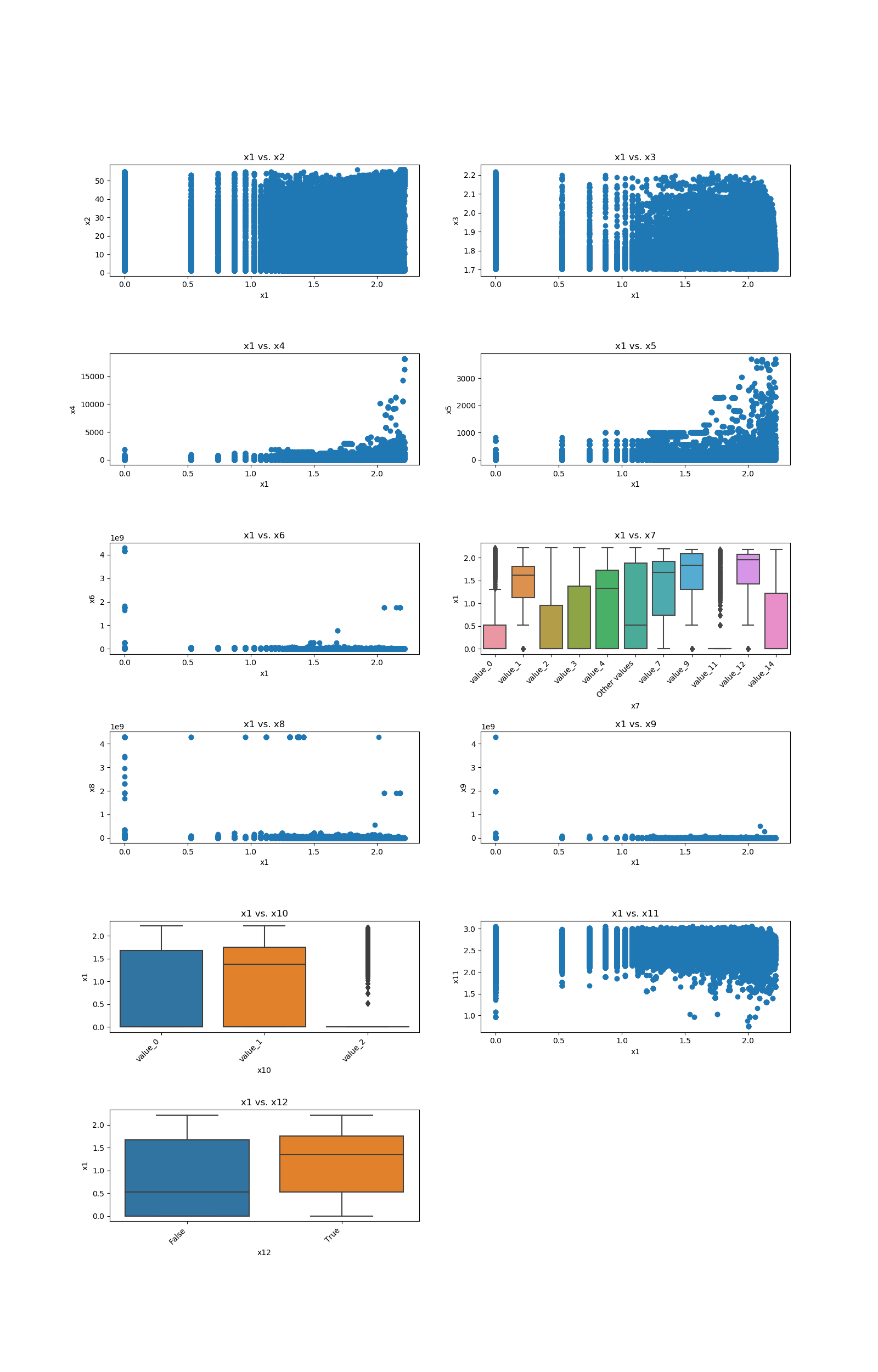
This code example shows how a loop can be constructed in order to show all of one feature relationship with all the others:

import pandas

from matplotlib import pyplot

from ds_utils.preprocess import plot_features_interaction


data_1M = pandas.read_csv(path/to/dataset)

figure, axes = pyplot.subplots(6, 2)
axes = axes.flatten()
figure.set_size_inches(16, 25)

feature_1 = "x1"
other_features = ["x2", "x3", "x4", "x5", "x6", "x7", "x8", "x9", "x10", "x11", "x12"]

for i in range(0, len(other_features)):
    axes[i].set_title(f"{feature_1} vs. {other_features[i]}")
    plot_features_interaction(feature_1, other_features[i], data_1M, ax=axes[i])

figure.delaxes(axes[11])
figure.subplots_adjust(hspace=0.7)
pyplot.show()

And the following image will be shown: