Unsupervised¶
The module of unsupervised contains methods that calculate and/or visualize evaluation performance of an unsupervised model.
Mostly inspired by the Interpet Results of Cluster in Google’s Machine Learning Crash Course. See more information here
Plot Cluster Cardinality¶
-
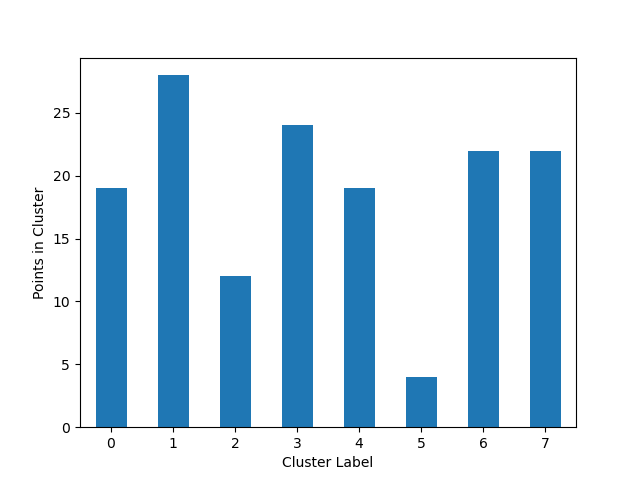
unsupervised.plot_cluster_cardinality(labels: numpy.ndarray, *, ax: Optional[matplotlib.axes._axes.Axes] = None, **kwargs) → matplotlib.axes._axes.Axes[source]¶ Cluster cardinality is the number of examples per cluster. This method plots the number of points per cluster as a bar chart.
Parameters: - labels – Labels of each point.
- ax – Axes object to draw the plot onto, otherwise uses the current Axes.
- kwargs –
other keyword arguments
All other keyword arguments are passed to
matplotlib.axes.Axes.pcolormesh().
Returns: Returns the Axes object with the plot drawn onto it.
In following examples we are going to use the iris dataset from scikit-learn. so firstly let’s import it:
from sklearn import datasets
iris = datasets.load_iris()
x = iris.data
We’ll create a simple K-Means algorithm with k=8 and plot how many point goes to each cluster:
from matplotlib import pyplot
from sklearn.cluster import KMeans
from ds_utils.unsupervised import plot_cluster_cardinality
estimator = KMeans(n_clusters=8, random_state=42)
estimator.fit(x)
plot_cluster_cardinality(estimator.labels_)
pyplot.show()
And the following image will be shown:
Plot Cluster Magnitude¶
-
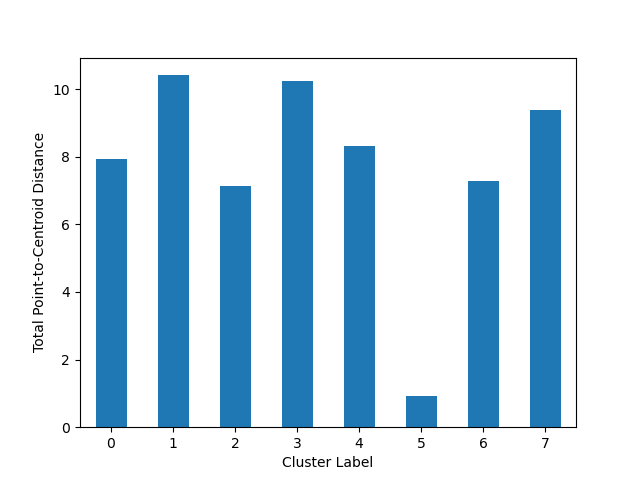
unsupervised.plot_cluster_magnitude(X: numpy.ndarray, labels: numpy.ndarray, cluster_centers: numpy.ndarray, distance_function: Callable[[numpy.ndarray, numpy.ndarray], float], *, ax: Optional[matplotlib.axes._axes.Axes] = None, **kwargs) → matplotlib.axes._axes.Axes[source]¶ Cluster magnitude is the sum of distances from all examples to the centroid of the cluster. This method plots the Total Point-to-Centroid Distance per cluster as a bar chart.
Parameters: - X – Training instances.
- labels – Labels of each point.
- cluster_centers – Coordinates of cluster centers.
- distance_function – The function used to calculate the distance between an instance to its cluster center. The function receives two ndarrays, one the instance and the second is the center and return a float number representing the distance between them.
- ax – Axes object to draw the plot onto, otherwise uses the current Axes.
- kwargs –
other keyword arguments
All other keyword arguments are passed to
matplotlib.axes.Axes.pcolormesh().
Returns: Returns the Axes object with the plot drawn onto it.
Again we’ll create a simple K-Means algorithm with k=8. This time we’ll plot the sum of distances from points to their centroid:
from matplotlib import pyplot
from sklearn.cluster import KMeans
from scipy.spatial.distance import euclidean
from ds_utils.unsupervised import plot_cluster_magnitude
estimator = KMeans(n_clusters=8, random_state=42)
estimator.fit(x)
plot_cluster_magnitude(x, estimator.labels_, estimator.cluster_centers_, euclidean)
pyplot.show()
And the following image will be shown:
Magnitude vs. Cardinality¶
-
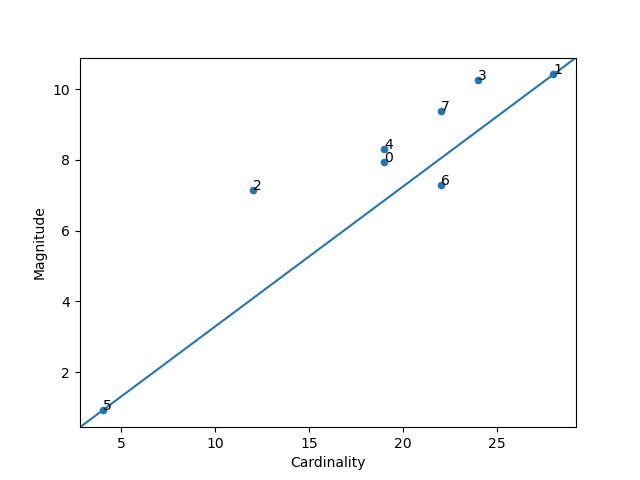
unsupervised.plot_magnitude_vs_cardinality(X: numpy.ndarray, labels: numpy.ndarray, cluster_centers: numpy.ndarray, distance_function: Callable[[numpy.ndarray, numpy.ndarray], float], *, ax: Optional[matplotlib.axes._axes.Axes] = None, **kwargs) → matplotlib.axes._axes.Axes[source]¶ Higher cluster cardinality tends to result in a higher cluster magnitude, which intuitively makes sense. Clusters are anomalous when cardinality doesn’t correlate with magnitude relative to the other clusters. Find anomalous clusters by plotting magnitude against cardinality as a scatter plot.
Parameters: - X – Training instances.
- labels – Labels of each point.
- cluster_centers – Coordinates of cluster centers.
- distance_function – The function used to calculate the distance between an instance to its cluster center. The function receives two ndarrays, one the instance and the second is the center and return a float number representing the distance between them.
- ax – Axes object to draw the plot onto, otherwise uses the current Axes.
- kwargs –
other keyword arguments
All other keyword arguments are passed to
matplotlib.axes.Axes.pcolormesh().
Returns: Returns the Axes object with the plot drawn onto it.
Now let’s plot the Cardinality vs. the Magnitude:
from matplotlib import pyplot
from sklearn.cluster import KMeans
from scipy.spatial.distance import euclidean
from ds_utils.unsupervised import plot_magnitude_vs_cardinality
estimator = KMeans(n_clusters=8, random_state=42)
estimator.fit(x)
plot_magnitude_vs_cardinality(x, estimator.labels_, estimator.cluster_centers_, euclidean)
pyplot.show()
And the following image will be shown:
Optimum Number of Clusters¶
-
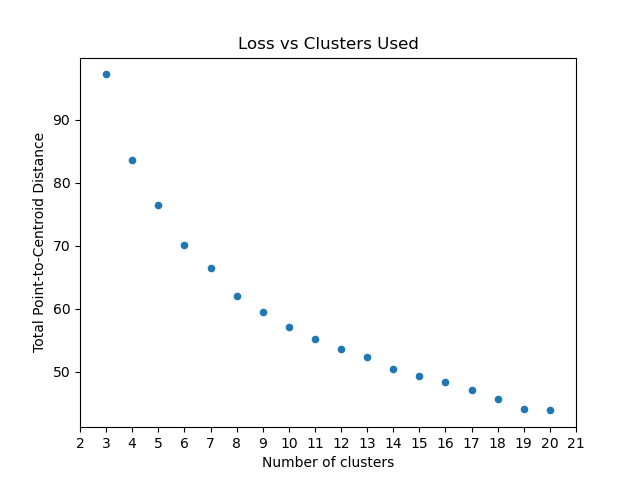
unsupervised.plot_loss_vs_cluster_number(X: numpy.ndarray, k_min: int, k_max: int, distance_function: Callable[[numpy.ndarray, numpy.ndarray], float], *, algorithm_parameters: Dict[str, Any] = None, ax: Optional[matplotlib.axes._axes.Axes] = None, **kwargs) → matplotlib.axes._axes.Axes[source]¶ k-means requires you to decide the number of clusters
kbeforehand. This method runs the KMean algorithm and increases the cluster number at each try. The Total magnitude or sum of distance is used as loss.Right now the method only works with
sklearn.cluster.KMeans.Parameters: - X – Training instances.
- k_min – The minimum cluster number.
- k_max – The maximum cluster number.
- distance_function – The function used to calculate the distance between an instance to its cluster center. The function receives two ndarrays, one the instance and the second is the center and return a float number representing the distance between them.
- algorithm_parameters – parameters to use for the algorithm. If None, deafult parameters of
KMeanswill be used. - ax – Axes object to draw the plot onto, otherwise uses the current Axes.
- kwargs –
other keyword arguments
All other keyword arguments are passed to
matplotlib.axes.Axes.pcolormesh().
Returns: Returns the Axes object with the plot drawn onto it.
Final plot we ca use is Loss vs Cluster Number:
from matplotlib import pyplot
from scipy.spatial.distance import euclidean
from ds_utils.unsupervised import plot_loss_vs_cluster_number
plot_loss_vs_cluster_number(x, 3, 20, euclidean)
pyplot.show()
And the following image will be shown: